Post
Morpho-Genesis 1980
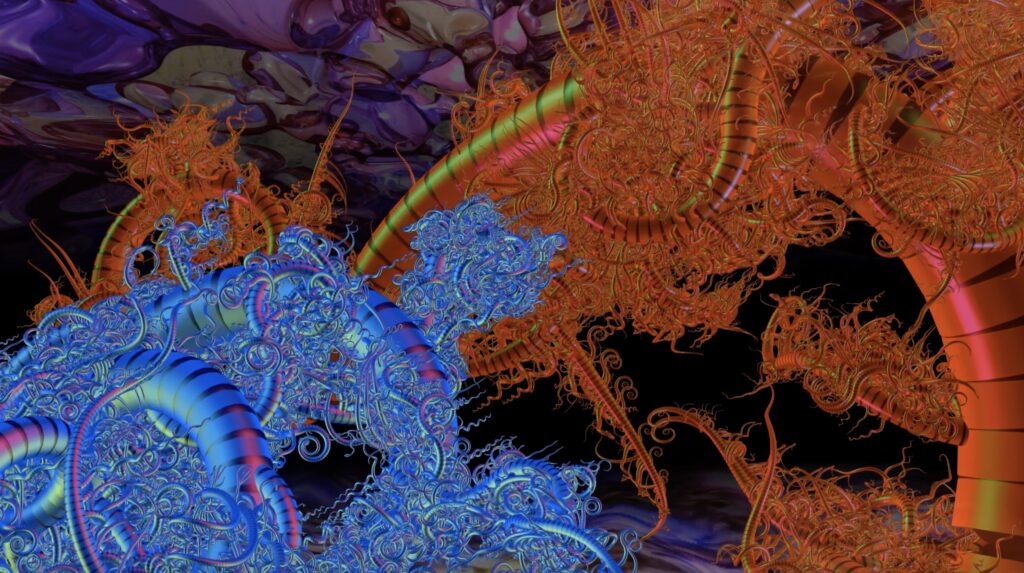
ITA I Growth Tendril sono opere tridimensionali create con la grafica computerizzata, introdotte durante l’annuale SIGGRAPH negli Stati Uniti nel 1982. Queste opere si basano sulla teoria del growth model di Kawaguchi. Oltre ai colori ricchi e al design unico, le opere contengono molti concetti geometrici che implicano la bellezza della matematica; ad esempio, il ricciolo delle foglie di felce e la spirale delle conchiglie marine sono applicati al principio della spirale logaritmica come i cerchi; le spirali logaritmiche hanno una simmetria perfetta, che conferisce loro un aspetto bello ed elegante come se stessero spiraleggiando senza gravità.
I viticci danzanti, simili a tentacoli, complicati e densi sul corallo e sulle conchiglie danno allo spettatore un senso di oppressione.
Si tratta di un’applicazione del concetto geometrico di frattale sviluppato dal matematico Benoit Mandelbrot negli anni ’70, in cui rami semplici continuano a ramificarsi come un’evoluzione complessa per formare strati multipli, formando infine un aspetto complesso con strutture ripetute uniche.Si tratta di un’auto-iterazione attraverso metodi ricorsivi. Pertanto, le somiglianze con se stessi all’interno della struttura ricorsiva/iterativa sottolineano l’infinita delicatezza del frattale. In altre parole, ogni elemento è una rappresentazione dell’intera forma. La forma complessiva mostra organicamente un’estetica mobile e distinta da quella precedente attraverso il cambiamento di ogni elemento costituito.
Tutte le evoluzioni sistematiche e le forme di crescita nel mondo naturale sono essenzialmente strutture iterative di un qualche principio, come i cristalli di neve, i rami degli alberi, i sistemi vascolari, le coste marine, i bordi delle nuvole e persino i fulmini nel cielo. Kawaguchi Yoichiro utilizza questo principio per indagare i bordi curvi, le strutture delicate e le forme complesse non solo attraverso la geometria statica, ma anche attraverso i cambiamenti dinamici della forma.
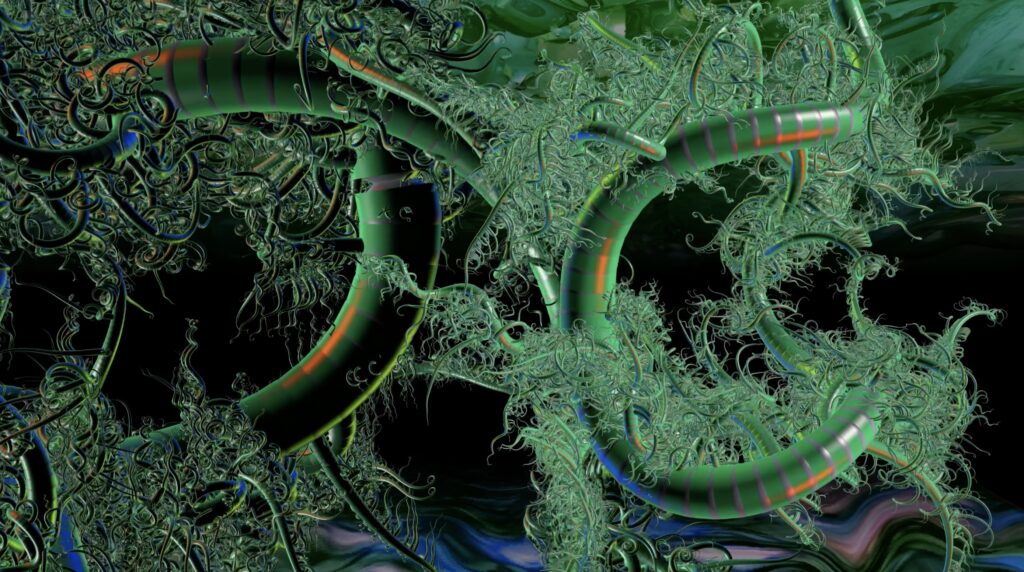
ENG Growth Tendril are three-dimensional works created with computer graphics that were introduced during the annual SIGGRAPH in the US in 1982. These works are based on Kawaguchi Yoichiro’s Growth Model theory. Apart from the rich colors and unique design, the works contain many geometric concepts that entail the beauty of mathematics; for instance, applied in the curl of fern leaves and the spiral of sea shells is the principle of logarithmic spiral like circles, logarithmic spirals have perfect symmetry, giving it a beautiful and elegant appearance as if spiraling without gravity.
The dancing, tentacle-like, complicated and dense tendrils on the coral and shells give viewers a sense of oppression. This is an application of the geometric concept Fractal developed by mathematician Benoit Mandelbrot in the 70s, where simple branches continue to branch out like complex evolution to form multiple layers, finally forming a complex appearance with unique repeating structures. This is self-iteration through recursive methods. Therefore, the similarities to themselves within the recursive/iterative structure stress the infinite delicacy within the fractal. In other words, each element is a representation of the entire form. The overall form organically displays a mobile aesthetic distinct from before through the change of each constituted element.
All systematic evolution and form of growth in the natural world are essentially iterative structures of some sort of principle, Such as snow crystals, tree branches, vascular systems, sea coasts, the edges of clouds, and even lightning bolts in the sky. Kawaguchi Yoichiro uses this to investigate curved edges, delicate structures, and complex shapes not only through static geometry but also through the dynamic changes of form.
Growth Tendril, 1980
